Die spitzen Klammern deuten an, dass es sich um ein geordnetes Paar handelt. Ein geordnetes Paar ist einer Menge ähnlich, jedoch ist in einer Menge die Reihenfolge der Elemente gleichgültig, in einem geordneten Paar nicht. Mit anderen Worten, die Mengen {Wien, Stixneusiedl} und {Stixneusiedl, Wien} sind identisch; die Paare ⟨Wien, Stixneusiedl⟩ und ⟨Stixneusiedl, Wien⟩ sind unterschiedliche Paare.

In der Tat ist die einzige Forderung, die man an ein Paar stellt, folgende:

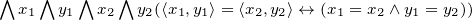
$∧ ∧ ∧ ∧ x1 y1 x2 y2(⟨x1,y1⟩= ⟨x2,y2⟩↔ (x1 = x2∧y1 = y2))$

Obwohl in einer Menge die Reihenfolge der Elemente gleichgültig ist, lässt sich das geordnete Paar auf eine Menge zurückführen: Die Menge {{x},{x,y}} erfüllt die vorher genannte Anforderung und ist damit eine adäquate Formulierung des geordneten Paars. Wer Lust dazu hat, möge versuchen, das zu beweisen.